Soil Mechanics
Maximiliano Garnier-Villarreal
2022-06-02
Source:vignettes/soil_mechanics_vig.Rmd
soil_mechanics_vig.RmdThis document highlights some functions of the GMisc package related to soil mechanics problems.
Bearing capacity
The idea here is to provide a function that solves the bearing capacity equation for different types of footings, giving as a result the allowable bearing capacity (\(q_a\)):
\[ q_a = \frac{0.5 \ B \ \gamma \ N_{\gamma} \ s_{\gamma} + D \ \gamma \ N_q + c \ N_c \ s_c}{FS} \]
where \(B\) is the width in meters, \(D\) is the embedment depth in meters, \(FS\) is the desired factor of safety, \(c\) is the cohesion in kPa (referred as tau0 in the function), \(\gamma\) is the unit weight in \(kN/m^3\), and the rest of the parameters are correction factors dependent on these input values, the internal friction angle \(\phi\), the type of footing (“strip”, “square”, “rectangular”,“circular”), and the depth to the water level.
The function that solves the above equation is bearing_capacity, with the mentioned arguments but specifying the wet unit weight, saturated unit weight for their respective use. The function outputs a table and graph for the results.
The B and D parameters can be vectors for multiple cases comparisons or single values for a single case estimate. If FS = 1 then the allowable and ultimate bearing capacities are the same (\(qa = qu\)).
Different scenarios can be analyzed:
- For a total stress analysis (TSA) in a cohesive soil (plastic silts and clays) set the friction angle equal to zero (
phi = 0) and the cohesion equal to the undrained shear strength (tau0 = Su). - For an effective stress analysis (ESA) in a cohesive soil use the effective friction angle (\(\phi'\)) and effective cohesion (\(c'\)).
- For a coarse-grained soil (gravels, sands, and non-plastic silts) usually TSA = ESA, and the friction angle and cohesion should be used, and if the material has no-cohesion then set cohesion equal to zero (
tau0 = 0)
We can define a set of parameters to use in different examples as follows:
B = seq(0.5, 2, 0.25)
D = seq(0, 2, 0.25)
L = NULL
gamma.h = 15.5
gamma.s = 18.5
tau0 = 10
phi = 30
FS = 3
wl = 1The first example uses the default “strip” footing:
bearing_capacity(B, D, L, gamma.h, gamma.s, tau0, phi, wl, FS)## $Result
## # A tibble: 9 × 8
## `D/B` `0.5` `0.75` `1` `1.25` `1.5` `1.75` `2`
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0 150. 163. 176. 160. 168. 175. 182.
## 2 0.25 179. 192. 182. 189. 197. 204. 211.
## 3 0.5 208. 204. 211. 218. 226. 233. 240.
## 4 0.75 225. 233. 240. 247. 255. 262. 269.
## 5 1 254. 262. 269. 276. 284. 291. 298.
## 6 1.25 220. 227. 234. 242. 249. 256. 264.
## 7 1.5 236. 243. 251. 258. 265. 272. 280.
## 8 1.75 252. 260. 267. 274. 281. 289. 296.
## 9 2 269. 276. 283. 290. 298. 305. 312.
##
## $Plot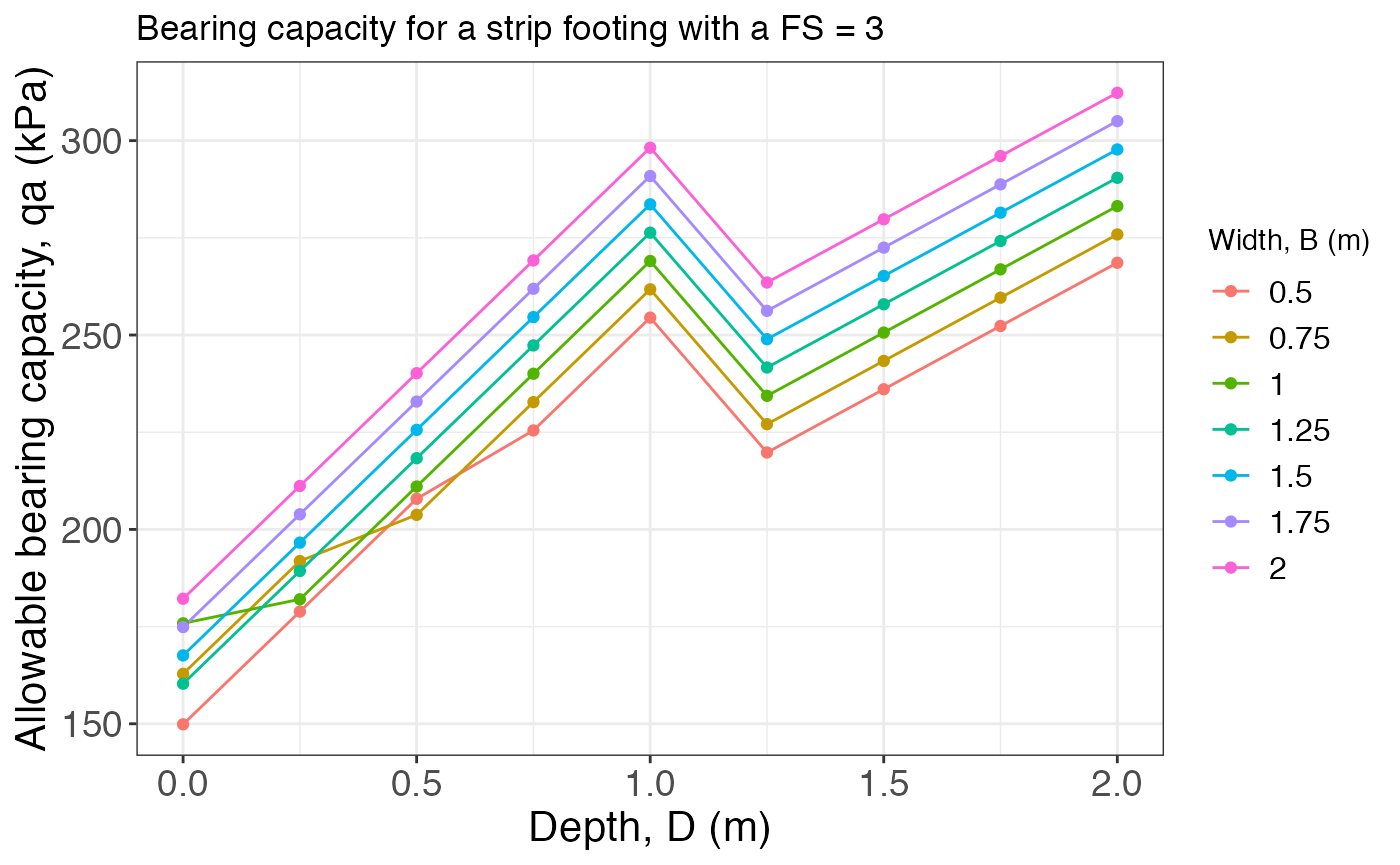
The second example uses the a “square” footing:
bearing_capacity(B, D, L, gamma.h, gamma.s, tau0, phi, wl, FS, footing = "square")## $Result
## # A tibble: 9 × 8
## `D/B` `0.5` `0.75` `1` `1.25` `1.5` `1.75` `2`
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0 182. 192. 203. 190. 196. 202. 208.
## 2 0.25 211. 221. 213. 219. 225. 231. 237.
## 3 0.5 240. 237. 242. 248. 254. 260. 266.
## 4 0.75 260. 266. 271. 277. 283. 289. 295.
## 5 1 289. 295. 300. 306. 312. 318. 324.
## 6 1.25 254. 260. 266. 272. 277. 283. 289.
## 7 1.5 270. 276. 282. 288. 294. 299. 305.
## 8 1.75 287. 292. 298. 304. 310. 316. 322.
## 9 2 303. 309. 314. 320. 326. 332. 338.
##
## $Plot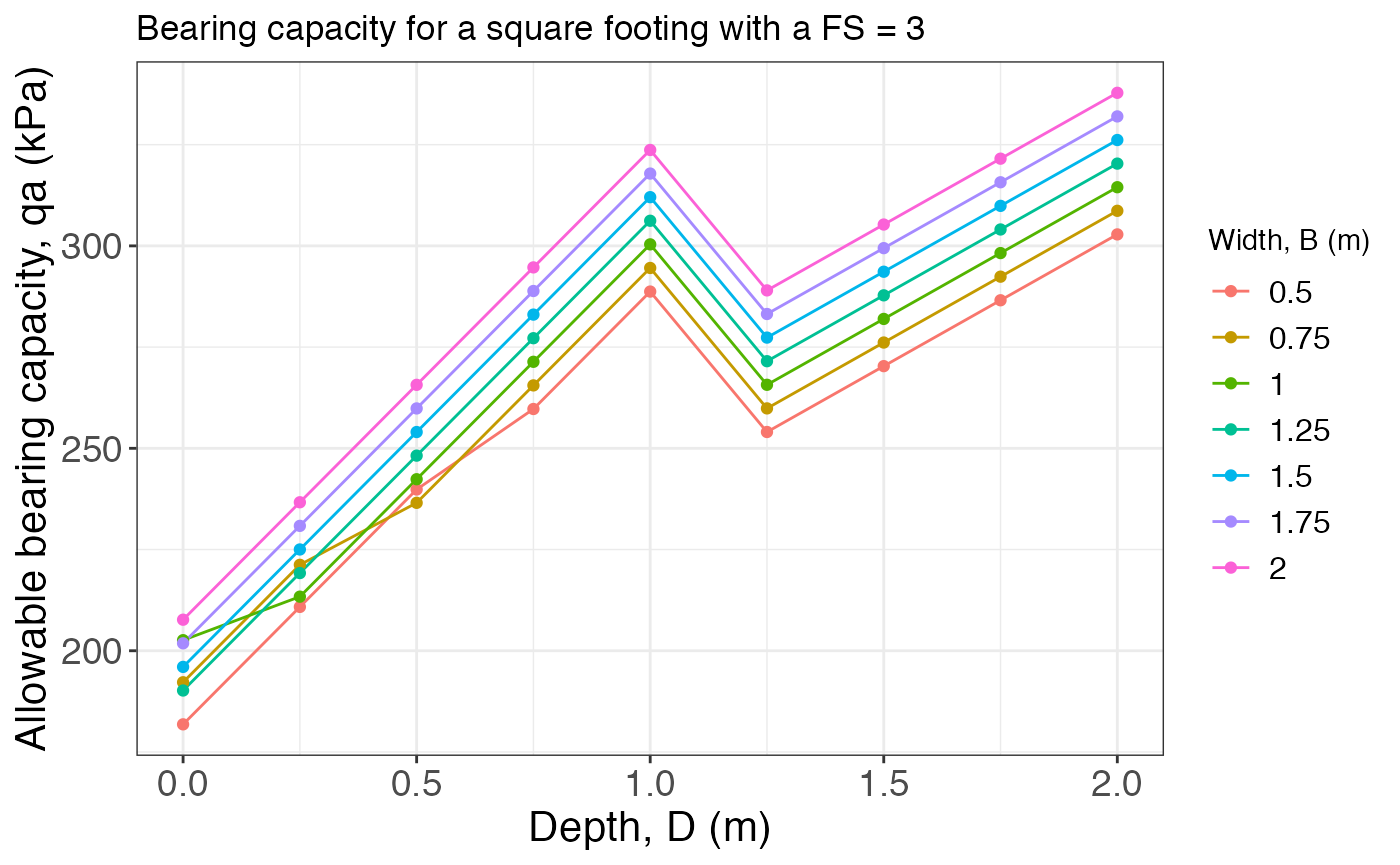
And the last example uses a “rectangular” footing, where is needed to define the L argument (the length of the footing in meters):
bearing_capacity(B, D, L = 3, gamma.h, gamma.s, tau0, phi, wl, FS, footing = "rectangular")## $Result
## # A tibble: 9 × 8
## `D/B` `0.5` `0.75` `1` `1.25` `1.5` `1.75` `2`
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0 151. 161. 172. 159. 165. 171. 177.
## 2 0.25 180. 190. 182. 188. 194. 200. 206.
## 3 0.5 209. 206. 211. 217. 223. 229. 235.
## 4 0.75 229. 235. 240. 246. 252. 258. 264.
## 5 1 258. 264. 269. 275. 281. 287. 293.
## 6 1.25 223. 229. 235. 241. 246. 252. 258.
## 7 1.5 239. 245. 251. 257. 263. 268. 274.
## 8 1.75 256. 261. 267. 273. 279. 285. 291.
## 9 2 272. 278. 284. 289. 295. 301. 307.
##
## $Plot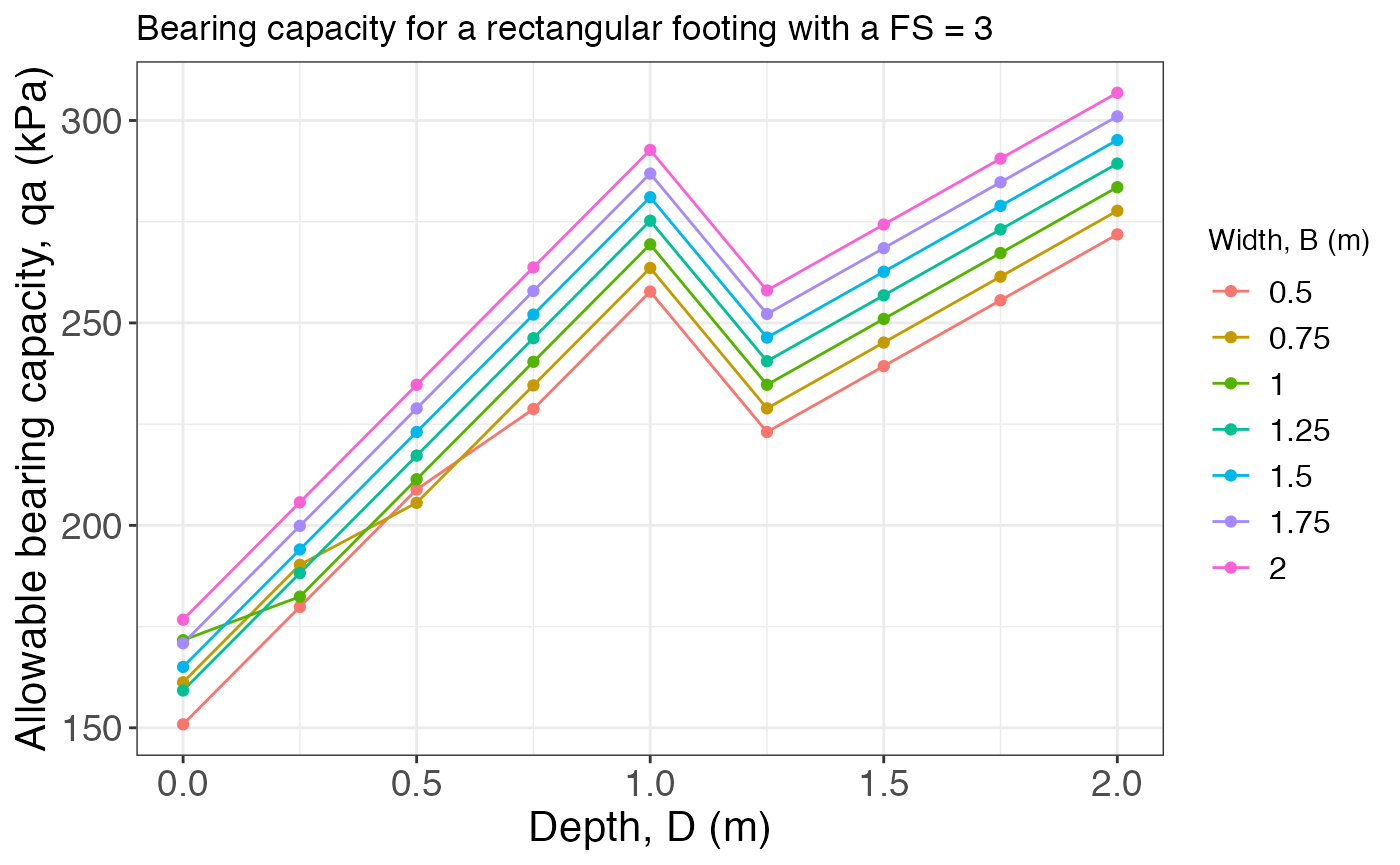
Induced stress
The function induced_stress calculates and plots the stress distribution under the center of a footing of different shapes (“strip”, “square”, “rectangular”, “circular”), using the solutions from Boussinesq. The arguments of the function are qs: the stress applied by the footing, B: the width of the footing in meters, L: the length of the footing in meters (applies only for rectangular footings), and z.end: the depth down to which calculate the stress. The function returns two plots: one static ($Plot) and one interactive ($Plotly), the last one is the one shown here.
The first example shows the plot for the default “strip” footing, and one value of width:
qs = 1
B = 1
L = NULL
z.end = 8
induced_stress(qs, B, L, z.end)$PlotlyThe second example plots the results for a “square” footing and different widths:
qs = 1
B = c(1, 2, 4)
L = NULL
z.end = 8
induced_stress(qs, B, L, z.end, footing = "square")$PlotlyThe last example plots the results for a “rectangular” footing and different lengths:
qs = 1
B = 1
L = c(1, 2, 4)
z.end = 8
induced_stress(qs, B, L, z.end, footing = "rectangular")$PlotlyDirect shear
The functions for direct shear are more for visualizing the results rather than to process the. The user should analyze the raw data and provide the normal stress (sig.n) - shear stress pairs (tau).
The first function plots the resulting \((\sigma,\tau)\) pairs and adds a line of best fit for the Mohr-Coulomb criterion (\(\tau=c+\sigma_n tan\phi\)). If the line of best fit estimates an intercept of less than 0 (\(c<0\)), the function automatically assigns \(c=0\), as this is not a possible solution. Also, the estimated parameters (\(c,\phi\)) are added to the plot.
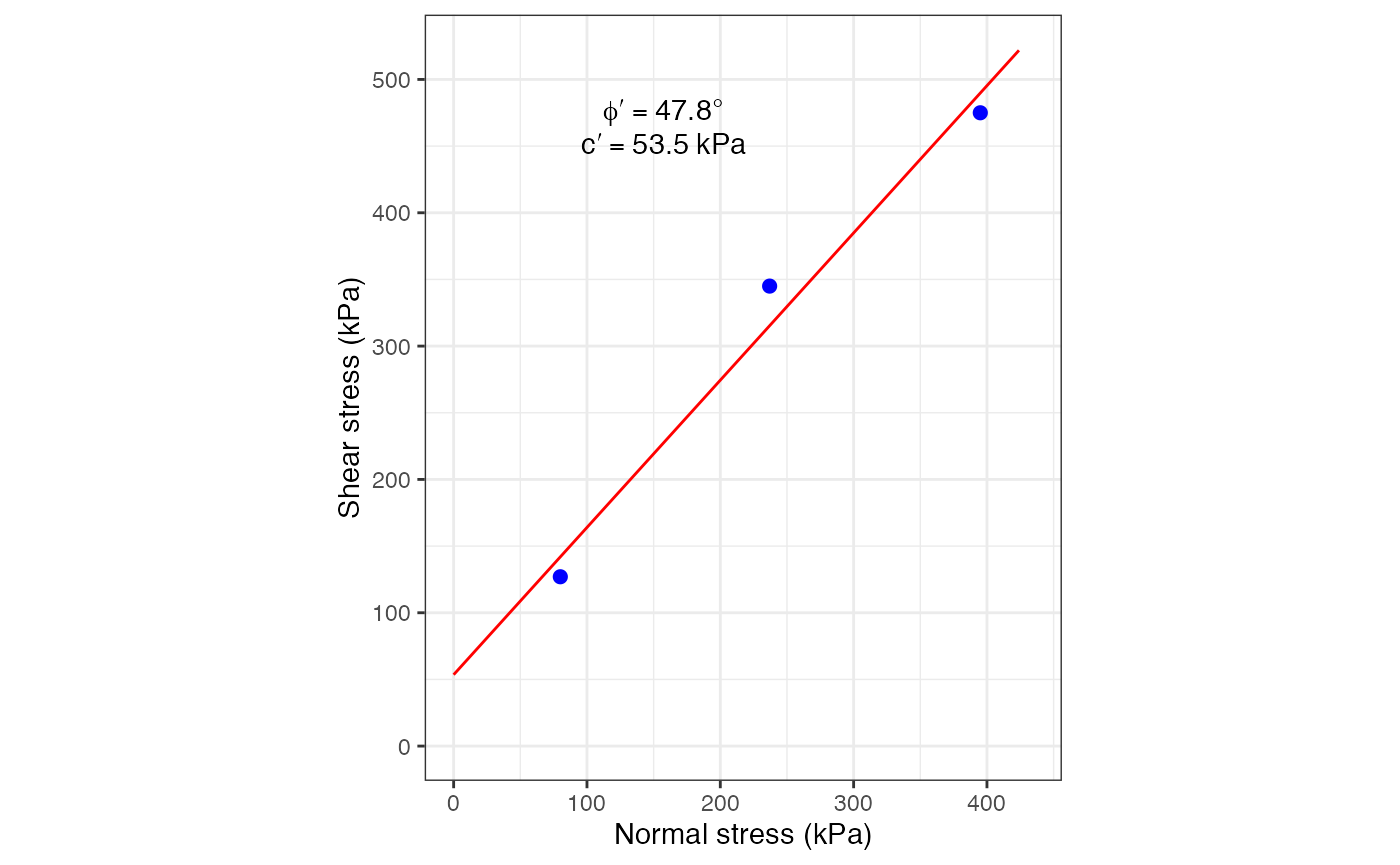
The second function adds on top of the first one by drawing the Mohr circles for each of the \((\sigma,\tau)\) pairs.
DS_Mohr_plot(sig.n = c(80,237,395), tau = c(127,345,475))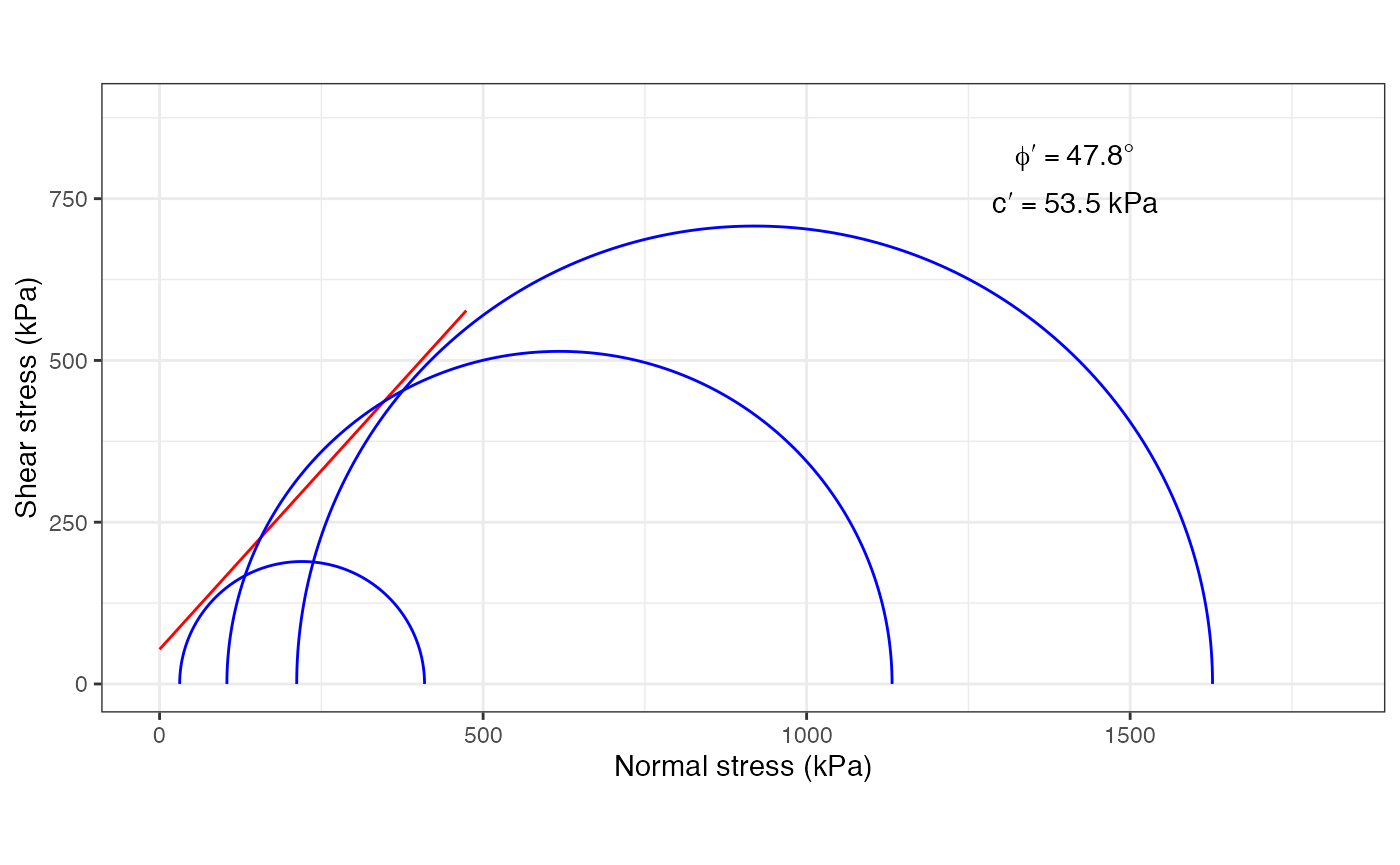
Mohr circle
The idea here is to provide a way to solve simple Mohr circle’s problems for the given normal stresses, shear stress, and rotation angle. The function returns a plot and the results for the given problem and parameters.
We can define some values to use:
sigx = 143.6
sigy = 100.5
tauxy = -14.4
theta = -35where sigx corresponds to the mayor normal stress, sigy corresponds to the minor normal stress, tauxy corresponds to the shear stress, and theta is the rotation angle for which to find the stresses.
In the first example the rotation is not applied:
Mohr_Circle(sigx, sigy, tauxy)## $results
## sig1 sig2 sig_theta tau_theta tau_max
## 1 147.97 96.132 143.6 -14.4 25.918
##
## $figure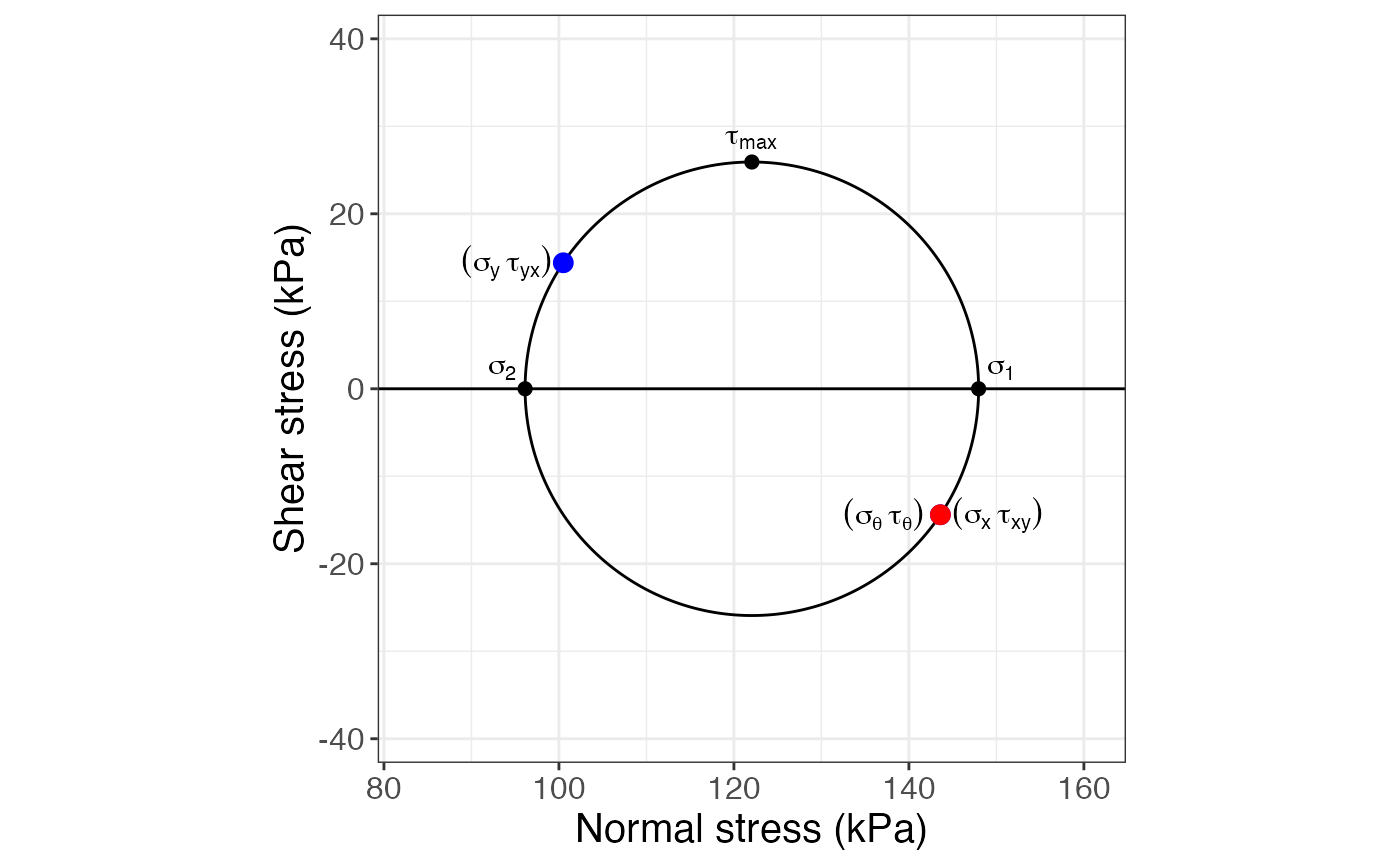
In the second example the rotation is applied:
Mohr_Circle(sigx, sigy, tauxy, theta)## $results
## sig1 sig2 sig_theta tau_theta tau_max
## 1 147.97 96.132 115.89 -25.175 25.918
##
## $figure
Shinyapp
A shinyapp using these functions can be accessed at https://maximiliano-01.shinyapps.io/soil_mechanics/.